НОВОГОДНИЙ КОНКУРС - 2004
Предлагаем Вашему вниманию задания очередного НОВОГОДНЕГО конкурса сайта "Тавлеи". (Редакция сайта выражает благодарность Петру Александровичу ШКЛУДОВУ за организацию данного конкурса по просьбам посетителей "Тавлей").
В заданиях №№ 1 - 3 - ход и выигрыш белых.
В задании № 4 - замените 6 черных шашек белыми, (какие - это вам как раз и надо решить!), и белыми же проведите выигрывающую комбинацию. Одно условие: шашек под боем быть не должно!
В задании № 5 - получите данную позицию (немного похожую на новогоднюю елку), из начальной расстановки шашек, за наименьшее количество ходов - при подведении итогов это будет учитываться (за самое короткое решение - 5 очков!)
КАК РЕШАТЬ ПОДОБНЫЕ ЗАДАНИЯ ВЫ МОЖЕТЕ ПОСМОТРЕТЬ В ИТОГАХ ПРЕДЫДУЩЕГО НОВОГОДНЕГО КОНКУРСА - 2003. ДА И "ЕЛОЧКА" ОСТАЛАСЬ ПОЧТИ ПРЕЖНЕЙ...
В задании № 6 - ход белых, запереть простую черных.
За указание полного побочного решения и нерешаемости дополнительно будут начисляться очки, по одному; за указание частного побочного решения - по 0,5 очка; за указание двойственностей, перестановок ходов - по 0,1 очка; за указание совпадений - по 0,5 очка.
Решения направляйте по электронному адресу: shkludov@aport.ru , с указанием в теме (subject) письма: "Новогодний конкурс - 2004".
Срок присылки решений - до 01.03.2004 г..
Победителей ждут призы! - комплекты электронного журнала "ТАВЛЕИ" за 2002-2003 года, а также шашечная литература.
Новогодний сюрприз: Призовой ФОНД конкурса - 50 долларов США !!
Желаем успеха!
Ниже опубликованы итоги конкурса: решения заданий, комментарии а также таблица результатов участников.
1. П.Шклудов, Новополоцк, Беларусь
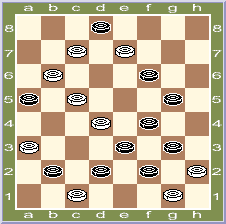 Выигрыш ( 3 очка )
Выигрыш ( 3 очка )
|
2. Р.Валеев, Пермь, Россия
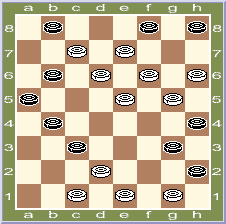 Выигрыш ( 3 очка )
Выигрыш ( 3 очка )
|
3. В.Волков, Новокузнецк, Россия
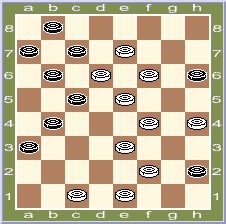 Выигрыш ( 3 очка )
Выигрыш ( 3 очка )
|
4. П.Шклудов, Новополоцк, Беларусь
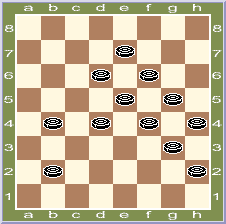 Заменить 6 шашек белыми. Выигрыш ( 3 очка )
Заменить 6 шашек белыми. Выигрыш ( 3 очка )
|
5. П.Шклудов, Новополоцк, Беларусь
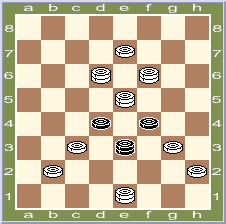 Получить позицию из начальной ( 5 - 1 очко )
Получить позицию из начальной ( 5 - 1 очко )
|
6. П.Шулев
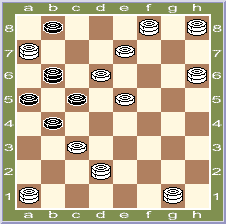 Запереть простую черных
Запереть простую черных( 3 очка ) |
РЕШЕНИЯ ЗАДАНИЙ, КОММЕНТАРИИ, ИТОГИ
№ 1.
b8, h8, e5, h6, c:e3, c1 (e3 A), g7 (c3), h8 (cd2), f2, e3, c3 +
A (dc3), g7 (a3), f8 (cb2 B), b4, a3 (d4), f2 (c3), e3 +
B (d4), g7 (e3), a1 + [3,0].
№ 2.
cd8 (f2 A B), e3 (g1), [Ч.п/р] f2, d4, hg7, g7, f8, f8*g5, a7 (c3), f2 (b4), e1 (a7 C), g3 (a3), e5 (ab2, d2), c3, c5 +
A (c5), hg7, f8, a3, b4, f8 (f2), g3 (f4), f6, h6 +
B (a7), b2, c3 (d2), c3, c3 (f2, g1), ed4, b4, d4, a3, g5/h4 +
C (c7), h4! [g3? (a3, ab2, d2) =] (a3), f6 (ab2, d2), c3, c5 + [3,0].
[Частное п/р] 3.d4, e3 (g1), d6-c7 (f4), e3, a3, f8 + [+ 0,5].
№ 3.
[П.п/р] g3 (g1 A B), d4, f2 (e3 C D), d8, d6 (e5), d6, b2, f4, d8 +
A (d4), c5, a5, f8 (b6, d6), c5 (g1), b4, f2, h8 +
B (a5), d4, ed2, g3, h8 +
C (c5), f4, g7, d8, a5 (d6), a*g7, g3 (e7), e1 (b6), c3 (a7), g5 (c5), h6 (d6), hg7 +
D (d4, g7), h8 (c5), d8 + [3,0].
[Полное п/р] 1.cd2 (d4), c5, a5 (g3), f8 (g1), de3 (g1-h2), f6-g7 (g1), h8 (b6), c7, b4, c3 (g1-h2), cd4 (b4), a1 (g1), h8 (g1-h2), ed4 (a3), c5 (g5), f6 (b2), h4 (c1), b6 + [+ 1,0].
№ 4.
Заменяем: d4, d6, e5, e7, f6, h2 белыми.
f8, c1, c7, b6 (e1 A), f2, f4 +
A (g1), a7 (g3, h2), b8 (e5), f4/h2 + [3,0].
[Второе решение]
А теперь, наоборот, заменяем: b2, b4, f4, g3, g5, h4 белыми.
c3, c5, f8, c1 (e5), I II hg5, g5/h6 (d4), d2 +
I b2 (f4), d4 +
II a3 (d4), b4 (e3), e1 + [+ 1,0].
№ 5.
- Вариант, приведенный Г.Магелинскасом (31 ход белых):
ab4 (dc5), (c5), b4, bc3 (fg5), h4 (f6), fg3 (c5), cd4 (ab6), dc3 (hg7), ed2 (a7), cb2, gf4 (e5), f4*b8 (de7), h4*h8 (cb4), (a3), d8 (c1), h4 (a3), e1 (a3-e7), c3 (h4), c5 (h4-g5), ed4 (c1), be5 (e7), hg3 (d6), e7 (g5), c5 (a3), cd6 (c1), c7 (e3), b8 (ab6), b2 (bc5), h2 (c5-d4), hf6 (gf4), bd6. [5,0].
- П.Римша и В.Гуделионис - по 43 хода. [по 3,5] (= (4+3)/2).
- А.Гимбутас - 44 хода. [2,0].
№ 6.
e1, d6*b4, a1*d4 (f2 A), g1*c1, b6, g3, d8 (a3 B), b4, b6, hd2, a5, d6, d6, b4, hb2.
A (e3), b6 (c7 C), c3, b2, a3, b4, h8-g7, d8 (a3 D), a5, c3, f2, d6, g5, dg3.
B (c3), b4, I II gh4!, a3, b4, e3, c5, dg5, h8-f6, d4, g3, g1.
C (c1), f4, eb4, c3, b6, fb4.
D (c3), b4, e5-f6, c5, fe7, f4, dg5. [3,0].
[Две двойственности]
I he3, a3, b4, gf2 [или h4], c5, g5, hd4, h4, g3, g1. [+ 0,1].
II f2, a3, b4, he3, c5, g5, hd4, h4, g3, g1. [+ 0,1].
Провокация?… Сколько дифирамбов спето этой задаче… Так почему бы не проверить её еще раз у хороших решателей? Задача "устояла"! Правда, к известной двойственности: I he3, добавилась более неприятная: II f2, в которой рисунок игры отличается от авторского еще больше. Но финал - тот же, и потому это не частное п/р, а только двойственность.
| № | Ф. И. О. | 1 | 2 | 3 | 4 | 5 | 6 | Очки | Место |
|---|---|---|---|---|---|---|---|---|---|
| 1 | А.Гимбутас, Утена, Литва | 3 | 3,5 | 4 | 4 | 2 | 3,2 | 19,7 | 2 |
| 2 | В.Сапежинский, Рогачев, Беларусь | 3 | 3 | 3 | 4 | - | 3,1 | 16,1 | 5 |
| 3 | П.Римша, Каунас, Литва | 3 | 3 | 3 | 4 | 3,5 | 3,1 | 19,6 | 3 |
| 4 | Г.Магелинскас, Биржай, Литва | 3 | 3 | 3 | 4 | 5 | 3,1 | 21,1 | 1 |
| 5 | В.Гуделионис, Каунас, Литва | 3 | 3 | 3 | 4 | 3,5 | 3 | 19,5 | 4 |
Таким образом, главный приз Новогоднего конкурса "ТАВЛЕЙ" - 50 долларов США - завоевал Гинтарас МАГЕЛИНСКАС, г.Биржай (Литва). Поздравляем !!
(для получения приза просим победителя связаться с Сергеем Старцевым по e-mail).
Примечание вебмастера.
Хочется подчеркнуть очень успешное выступление Г.Магелинскаса в конкурсах решений, освещаемых нашим сайтом. Так, он становится победителем Новогоднего конкурса "ТАВЛЕЙ" второй год подряд, а также занял второе место в Кубке Президента FMJD и - опережаю публикацию результатов - уверенно победил в конкурсе "ГРАНТ-2002", став при этом призером во всех (!!) номинациях, в которых участвовал.
Нельзя не отметить также обстоятельные и часто самые полные (в этом конкурсе - на три задания из шести!) ответы А.Гимбутаса. И только относительная неудача в одном из самых сложных - задании № 5 (построить данную позицию из начальной) - не позволила ему завоевать первый приз.
Но, вспомните, ведь в "Новогоднем конкурсе-2003" будущий победитель даже не стал приступать к аналогичному заданию, в чем честно признался, а теперь - просто блестяще справился с ним! (без чего бы, кстати, и не победил...) Это доказывает, насколько участие в подобных конкурсах обогащает самих решателей, позволяет им глубже проникать в "таинства" шашек.
Поэтому редакции не совсем понятно невысокое число участников в этом конкурсе, которое не увеличил и
неожиданный денежный приз. И, тем не менее, мы надеемся, что конкурс вам понравился.


