ВНИМАНИЕ !!! В позицию, опубликованную на этой странице ранее, вкралась досадная ошибка! (не по вине редакции). Просим извинения у наших посетителей за то, что увели "в сторону" Вашу творческую мысль...
Шашечная теорема Ферма
Гроссмейстер Вениамин ГОРОДЕЦКИЙ :
"Хочу предложить Вам провести конкурс из одной моей конструкции, возникшей в анализе (совсем недавно). Я, правда, колеблюсь: мне кажется, что позиция может быть некоей "шашечной теоремой Ферма" и быть достаточной для определения рейтинга шашечного мышления индивидуума. Ее можно предложить по Интернету. Позиция вот какая :
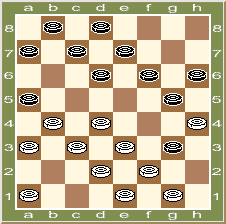 |
( Позиция уточнена самим автором ! ) Белые : a1, a3, b4, c3, d2, d4, e1, e3, f2, g1, h4 ( 11 ); Черные : a5, a7, b8, с7, d6, d8, e7, f6, g3, g5, h6 ( 11 ).
Определить результат борьбы.
Дополнительные вопросы :
|
| Ход белых. |
Я не даю решение, чтобы Вы могли оценить величие конструкции. Жду отклики."
В своем письме-уточнении Вениамин Городецкий утверждает, что "с этой позицией не справятся даже ведущие гроссмейстеры мира".
Это письмо Вениамин Городецкий прислал Юрию ГОЛОВКОВУ, редактору и издателю ежемесячной газеты "Донской шашечный листок", а Ю.Головков, в свою очередь, предложил поместить эту позицию на нашем сайте. ( Позиция была опубликована и в "ДШЛ" N 3 / 2002, и также с ошибкой ).
Характер исправления позиции ( напомним "прежнее" расположение черных шашек: a5, a7, b6, b8, d6, d8, e7, f4, f6, g5, h6 ) наталкивает на мысль, что на доске был ошибочно сделан последний ход черных - 1... cb6 вместо правильного 1... fg3. Может быть, автор считает исходной позицией ту, что была в партии на пол-хода раньше? Тогда и фраза первого дополнительного вопроса "при ходе белых не может" относится к этой позиции...
Редакция "Тавлей" постарается уточнить этот момент у самого автора.
Историческая справка.
Пьер ФЕРМА (1601 - 1665) - французский математик, один из создателей аналитической геометрии и теории чисел. Труды по теории вероятностей, исчислению бесконечно малых и оптике.
Теорема ФЕРМА - утверждение теории чисел, согласно которому уравнение xn + yn = zn при n > 2 не имеет целых положительных решений. Справедливость теоремы Ферма доказана для ряда показателей n, но в общем виде остается недоказанной *). Пьер Ферма, высказавший эту теорему, не оставил ее доказательства.
*) Прим. ред. Теорема Ферма была доказана лишь в 1995 г. Сколько же времени потребуется на доказательство "шашечной теоремы Ферма" ?!
Присылайте Ваши решения редактору или
вебмастеру.