Мы решили напечатать эту достаточно известную статью международного гроссмейстера Вениамина Городецкого, во-первых, потому, что разделяем стремление автора пропагандировать русские шашки, раскрывая их красоту путем глубокого проникновения в "тайны" позиции, а, во-вторых, - потому, что ей просто не место "на задворках" Интернета.

Мы также отдаем себе отчет, что тематика статьи близка и к разделу "Компьютерные шашки", но поместили ее здесь специально рядом с другим материалом В.Городецкого "Шашечная теорема Ферма".

Читайте также наше Послесловие редакции.

Квадриллионы операций или Поиск истины

"Истина - тайна, всегда тайна.
Очевидных истин не бывает".
А.Платонов

"Язык мозга не есть язык математики.
Кибернетике еще предстоит обучиться
говорить на языке мозга".
Дж.Нейман

В самой древней и вечно юной ветви математики - теории чисел - нередко появляются поразительно простые на первый взгляд задачи, решение которых годами, а подчас и столетиями, не поддается усилиям самых крупных ученых эпохи. Этому феномену был посвящен один из курсов лекций, прочитанный в МГУ видным математиком Александром Яковлевичем Хинчиным и названный им "Три жемчужины теории чисел". В приведенных решениях он пользовался простейшими приемами, и вместе с тем доказательства были чрезвычайно сложными и неимоверно красивыми. Мне посчастливи лось прослушать этот курс. Более полувека спустя я обнаружил аналогию в интеллектуальных играх.

Игры на Земле возникли вместе с человеком. Они и поныне сопутствуют друг другу. В физиологии существует мнение, что игры - врожденная, ничем не заменяемая потребность организма; без ее удовлетворения невозможно нормальное развитие мозга.

Многие выдающиеся умы прошлого придавали играм огромное значение. Любопытно, что в высказываниях и действиях некоторых из них проскальзывает идея "моделей".

Аналогичная ситуация складывается при любой игре, например русские шашки. Играющий белыми по одному ему ведомым причинам определяет свой первый ход из семи возможных. Уже после ответа противника возможно возникновение 49 позиций. В дальнейшем их количество нарастает лавинообразно, увеличиваясь со скоростью экспоненциальной (степенной) функции.

Вспоминается любопытная история. В 1959 году в одной турнирной партии, играя черными, я добился победы после напряженной многочасовой борьбы. Девять лет спустя скрупулезное исследование убедило меня, что позиция, возникающая после 1.gh4 ba5 2.ed4, уже для белых безнадежна. Публикация этого открытия вызвала настоящий переполох. И это естественно. Объем и глубина анализа были поистине поразительными. После нескольких ходов доказательство распадается на три системы. Только одна из них содержит 4,59x10³⁰полуходов.

Из такого же порядка полуходов состоят и две другие системы. Разве этот анализ не достоин Книги рекордов Гиннесса?

Продолжим основную тему. Прежде чем делать очередные ходы, соперники рассчитывают последствия: "он пойдет так, я отвечу так" (выбор может быть иным); при этом играющие стремятся в силу своего понимания учитывать лучшие ходы противника и выбирать лучшие ходы для себя. В итоге возникает информация, дающая возможность рассматривать лишь часть вариантов.

Такой подход в программировании был назван минимаксной процедурой [1] ("макси-" - лучшие собственные ходы, "мини-" - лучшие ходы противника, играющие для нас отрицательную роль). Как же оценить качество хода? Самый простой, но и самый объемный путь - просчитать до конца все варианты, возникающие после каждого хода, и выбрать тот, который кратчайшим путем ведет к достижению цели. Признаки окончания игры (достижения выигрыша, проигрыша или ничьей) составляют "терминальный узел". Понятно, что в таком случае никакого сокращения перебора быть не может. Сократить перебор удается только введением "модельного терминального узла", то есть внедрением признаков, характеризующих разбираемый вариант как бесперспективный, позволяющих прекратить его анализ задолго до достижения истинного терминального узла, то есть отсечь определенную часть ветвей дерева игры ("поддеревьев").

Таким образом, основная проблема, стоящая перед эвристическим программированием, - ограничение перебора, - казалось бы, решена. Однако ограничение перебора, сокращая трассу, создает угрозу того, что вместе с водой будет выплеснут и ребенок. Дело в том, что модельный узел может свидетельствовать или о детерминированном достижении определенного результата, или только о вероятности его достижения. Поэтому во втором случае не исключено возникновение ситуаций, когда вместо ожидаемого высоковероятного результата получается прямо противоположный. Например, стремление к материальному превосходству или хотя бы сохранению равновесия способно сыграть отрицательную роль; возможны ситуации, где простая сильнее дамки, а "отсталая" шашка выполняет самую активную функцию; стратегически оправданный захват центра нередко приводит к гибели из-за окружения и т.д.

Иллюстрацией к сказанному служит позиция, приведенная на диаграмме 1.

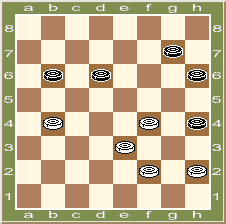
Диаграмма 1. Белые: b4, e3, f2, f4, h2  ( 5 ); Черные: b6, d6, g7, h4, h6  ( 5 ). Ход белых. Могут ли они достичь ничьей ?

Положение белых очень плохое: основные силы расположены на одном (правом) фланге, там же - пассивная шашка (h2); весьма ограничена маневренность. Каковы шансы белых на спасение? С помощью несложного анализа можно прийти к заключению, что первыми полуходами сторон должны быть ed4 и gf6, так как другие продолжения белых ведут к неизбежному поражению через несколько ближайших полуходов, а другие ответы черных дают возможность противнику достичь ничьей.

Итак, 1.ed4 gf6. Что дальше? Проведем прикидки (изучим возможные модельные терминальные узлы): 2.ba5 dc5 3.a:c7 c:g1 4.cb8 ga7 (лучший ход, ограничивающий действие дамки b8) 5.bc7 (или d6) fg5 6.fe5 ab8 7.cd6 gf4 8.e:g3 h:f2! (в случае 8... b:e5 следует 9.gf4, и белые достигают ничьей) 9.da3 be5. В теории известно, что этот эндшпиль для черных выигрышный (детерминированный модельный узел). Между прочим, первая прикидка состоит из 18 полуходов. Окончательная оценка требует еще определенных знаний теории или дополнительного увеличения анализа на огромное количество полуходов. В любом случае белым приходится отказаться от этого варианта (2.ba5), то есть данное поддерево следует отсечь и перейти к другому.

Если 2.fe3, то в ответ имеется два осмысленных хода 2... hg3 или 2... ba5. Оба варианта ведут к победе черных, хотя в первом случае выигрыш дается довольно легко (2... hg3 3.ba5 g:c3 4.a:g7 hf8 5.hg3 cb2 6.ed4 ba1 7.dc5 ae5 Х), а второй требует особого рассмотрения: 2... ba5 3.dc5 a:c3 4.c:g5 h:f6 5.hg3 cb2 6.ed4 fg5!! (парадоксально, что 6... bа1 к выигрышу не приводит) 7.de5 ge3 8.ed6 ed2! 9.dc7 de1! 10.gf4 ec3 11.cb8 cf6 Х. Анализ в 22 полухода содержит 1,5х10¹³ вариантов.

В сложившейся ситуации белым приходится искать нетривиальные продолжения. Таких разумных продолжений два: 2.fe5 и 2.fg3. В первом случае после 2... d:f4 3.ba5 fe3 4.a:c7 e:g1 оборона белых рушится. Остается последняя возможность: 2.fg3 h:f2 3.ba5. Теперь, если черные ответят 3... dc5, они даже проигрывают - 4.a:c7 c:g5 5.hg3! f:h4 6.cb8 Х. Не выигрывает и 3... fg5 4.a:e5 g:c5 5.hg3! f:h4 6.ef6, и в дальнейшей борьбе черные не могут реализовать огромный материальный перевес, так как белым удается овладеть большаком или отрезать две простые черные по линии двойника. Однако после 3.ba5 следуют одна за другой две неожиданные жертвы: 3... bc5! 4.d:b6 dc5! 5.b:d4 и после 5... fg1 спасения у белых нет. В самом деле, если попытаться организовать прорыв 6.de5 f:d4 7.ab6, то просто 7... de3; не спасает и попытка пожертвовать еще одну шашку 7.fg5, из-за того, что после 7... h:f4 8.ab6 следует 8... fg3 9.h:f4 de3 Х.

Казалось бы, анализ закончен, он почти везде доведен до истинного терминала. Осталась практически одна нерассмотренная возможность, которая на первый взгляд выглядит как модельный терминал и могла бы вообще не анализироваться. И все таки...

Вторая нетривиальная жертва - 3.hg3! f:h4 4.ba5, и черные, как следует из вышеприведенного разбора, выиграть не могут.

Как трудно дается игроку минимаксная процедура - основная работа шашиста-практика!

Итак, минимаксная процедура оценки значимости хода - определение модельного терминального узла - может выполняться различными путями. Первый заключается в использовании известных стандартных решений определенных универсальных ситуаций - детерминированных модельных терминальных узлов. (В связи с этим довольно давно еще в "Книге о шашках" я высказал мысль, что полезно было бы внести в банк данных играющего компьютера все исследованные "канонические" позиции.) Второй путь состоит в ориентировочной оценке позиции на основе общих представлений о стратегии и тактике игры, что позволяет с большей или меньшей вероятностью выбрать наиболее удачный ход - вероятностный модельный терминальный узел. Абсолютизацией первого подхода может служить третий путь - создание разветвленной базы данных.

Много лет собирает информацию для банка данных по русским шашкам петербургский кибернетик А.Аникеич. Любопытно, что еще с довоенного времени упомянутый нами московский шашист С.Голубев [2] разработал систему кодов к собственному каталогу, позволяющую быстро находить любую опубликованную шашечную позицию. В последующем эта система была модифицирована кандидатом в мастера Е.Каском.

Видный американский шахматный программист Дж.Шеффер, добившийся заметных успехов в создании "электронных гроссмейстеров", к шашкам (чекерс) относился с некоторой долей пренебрежения. Случай заставил его изменить отношение к этой игре. Теперь он занимается только ею. В университете Альберта в Эдмонтоне его сотрудники годами создавали банк данных, который содержит анализ всех позиций, начиная с минимального количества шашек (1 х 1), с последующим увеличением числа боевых единиц (сейчас анализ доведен до уровня 5 х 5). Дж.Шеффер утверждает: "Имея такие банки и доведя игру до положения, когда на доске останутся последние несколько шашек, программа может проанализировать все возможные варианты и выбрать оптимальную стратегию, которая либо приведет к победе, либо позволит отсрочить поражение..." Отметим, что это высказывание содержит две противоречивые тенденции. С одной стороны, тотальный анализ, содержащийся в банке данных, предоставляет для использования детерминированные модельные терминальные узлы и позволяет находить кратчайший путь к цели или, не доводя игру до истинного терминального узла, признать поражение. С другой - возможность "отсрочить поражение" предусматривает наличие такой программы, которая "надеется" на промах противника, то есть нарушает основной принцип минимаксной процедуры. Тем не менее уже сейчас программа играет на уровне чемпиона мира.

Кибернетики обнаружили, что шашки (как и шахматы) - удобный полигон для отработки и испытания новых концепций программирования, которые могут быть использованы в других областях. Недаром эти игры затрагивают душу человека. Сам Дж.Шеффер пишет: "Когда я занялся проблемой этой игры, мое уважение к ней намного возросло. Эта игра на самом деле невероятно сложная. Большинство людей и представить себе не может, насколько тонкой и элегантной игрой являются шашки".

Родоначальник детективной литературы, поэт, художник, математик, естествоиспытатель Эдгар По еще в 1841 году высказал мысль: "Так называемые аналитические способности нашего ума сами по себе недоступны анализу. Мы судим о них только по результатам. Среди прочего нам известно, что для человека, особенно одаренного в этом смысле, дар анализа служит источником живейшего наслаждения..."

Шашечный анализ в конечном счете сводится к перебору вариантов. Но только интуиция, озарение и чувство прекрасного ориентируют поиск в нужном направлении, придавая игре всю ее эстетическую насыщенность. Какое наслаждение может дать шашечный анализ, убедитесь сами - диаграмма 2.

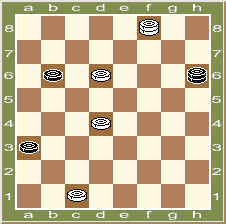
Диаграмма 2. Белые:  дамка f8,  простые c1, d4, d6  ( 4 ); Черные:  дамка h6,  простые a3, b6  ( 3 ). Ход белых. Выигрыш.

Эту позицию я предложил в качестве одного из заданий суперконкурса "Три жемчужины русских шашек", проведенного в конце прошлого года "Экспресс-газетой", перепечатанного нью-йоркским еженедельником "Русский Базар" и продублированного в Интернете [3]. Несмотря на большое число участников (из России, Украины, Америки, Бразилии), лишь одному удалось более или менее подойти к правильному решению. Обратимся к краткому анализу.

У белых огромное материальное, позиционное, пространственное превосходство. Еще два шага - и они получат вторую дамку. И очередь хода принадлежит им. Но у черных нежданно-негаданно появляются оборонительные ресурсы. Сумеют ли белые подавить их? Или им придется сделать хорошую мину при плохой игре и довольствоваться миром?

Чтобы найти первый ход, большого ума не надо, тем более что в случае 1.de5 bc5! черные овладевают большаком.

Итак, 1.de7. Что делать черным? Несложный анализ показывает, что полезных ходов у них нет. Сдаваться? Но тут возникает первый парадокс. При минимальных силах черные жертвуют свой главный козырь, и борьба разгорается с новой силой: 1... hd2!! 2.c:e3 ab2 3.de5. Чтобы рассчитывать на победу, годится только этот ход. 3... ba1 4.ed6 ab2.

Что дальше? Конечно, нельзя 5.ed8 из-за 5... bc1. Может быть, 5.ef4? Тогда 5... bc1 6.ed8 c:h6 7.da5 hf4 8.ac5 fc1 9.fg7 ch6 10.gb2 bc1! Сохранить большак и одновременно защитить шашку d6 белые не могут. Ничья. Очень любопытно, что после 5.ef4 у черных есть другой путь к спасению (его нашел гроссмейстер Е.Зубов), причем более сложный и, что гораздо важнее, более красивый: 5... be5 6.fg5 e:c7 7.gf6 (7.fg7 cd8 8.gf6 bc5 =) 7... cd8 8.fh6 bc5 9.hg5 (9.he3 da5 =) 9... cd4 10.gf4 dc3 11.fc1 db6 12.ef8 bf2. Ничья. Вы все поняли?

Вернемся к положению после четвертого хода черных. У белых есть блестящий труднонаходимый план. 5.fh6!! Можно показать, что последующий ответ черных вынужден. В самом деле, если черные оставят простую на b6, они уже никогда не пересекут линию тройника, а ход дамкой на c1 (5... bc1) бесперспективен из-за 6.hf4 bc5 7.d:b4 ca3 8.ba5 af8 9.fe5 Х. Поэтому 5... ba5 6.ed8! Возможности черных сужаются. В случае 6... ab4 следует 7.da5 ba3 (7... b2-c3 8.hf8 Х) 8.ad2, и надежды черных на проведение простой в дамки рушатся. У черной дамки на большаке остается единственная безопасная стоянка - поле h8.

6... bh8 7.ef4 (по большому счету проходит перестановка ходов - годится и 7.dc7) 7... ab4 8.d8-c7!! Ключевой момент уникального и глубочайшего плана. Смысл его станет ясен лишь после изучения приводимого варианта: 8.da5 ba3 9.dc7 (еще полшага к цели, а нужен целый шаг!) 9... ab2 (при других ходах черных прорваться шашке a3 не удастся) 10.ac3 bd4 11.fe5 df6 12.hg7 fg5 13.ga1 gf4 14.cd8 fe3 15.da5. Черные обречены? Решающий удар 16.ac3 неминуем? Ничего подобного! Черные жертвуют дамку на g7, или на f6, или даже на e5, и прорыв простой e3 обеспечивает ничью. У черных всего три боевые единицы, две они уже пожертвовали.

Итак, только 8.d8-c7!! Грозит уничтожение дамки h8 и черные вынуждены убрать ее на c3 8... hc3. Эта стоянка единственно приемлемая. Если 8... hd4, то 9.ca5 ba3 (9... dc3 10.hf8 Х) 10.ad2, и черные обречены.

Победа белых уже не за горами. Но необходим еще весьма тонкий ход: 9.de7 (не ведет к цели 9.cb8 bc3 10.fg5 из-за 10... cb4 11.de7 b:f8 12.be5 fe7 13.ef6 ed8 или f8 =) 9... ch8 (приходится возвращаться, и теперь нельзя 9... cd4 из-за 10.ca5 ba3 11.ad2 de3 12.ed8 Х).

Схватка завершена: 10.ef8 (или 10.ca5) 10... ba3 11.ca5 ab2 12.ac3 (12.fe5? h:c3! =) 12... b:d4 13.fe5 d:f6 14.hg7 (14.fg7? fg5 =) 14... fg5 15.ga1 gf4 16.fc5 fg3 17.cd4 h:c3 18. a:h2. Как видите, на оптимальной трассе нужно было найти 35 полуходов, а машине проанализировать 1,3х10²⁷ вариантов.

О чем бы мы ни думали, чем бы мы ни занимались, основной нашей задачей и главным методическим приемом оказывается сокращение перебора. Но ограничение вариантов может лишить нас эстетического наслаждения красотой оригинальных решений и неожиданных ходов.

Лишить той самой красоты, которая должна спасти мир. Если ее не уничтожит расчет.

Международный гроссмейстер,
академик Петербургской академии шахматного
и шашечного искусства
Вениамин ГОРОДЕЦКИЙ

[1] А. Л. Брудно. Грани и оценки для сокращения перебора вариантов. - "Проблемы кибернетики", 1963, # 10. Примерно в это же время такую же идею независимо высказал Дж. Маккарти.

[2] С. Голубев. "Мои карточки". Сборник бюллетеней XI Первенства СССР по шашкам, 1949.

[3] На ныне бездействующем сайте ФШР по адресу https://www.shashki.ru/win/sp_k_99.htm.

Статья публикуется с разрешения Ю.Головкова, редактора "Донского шашечного листка", где она была напечатана. Вы можете также найти ее в Интернете по адресу https://www.ug.ru/ug_pril/ol/2000/08/esience.htm.

Послесловие редакции

Статья В.Городецкого была написана в 1999 году, т.е. достаточно давно. И нам было интересно посмотреть на некоторые ее положения с точки зрения дня сегодняшнего.

Прежде всего, одно общее замечание. Хотя автор публикации и ссылается на фундаментальную работу А.Л.Брудно, говорит о мини-максной процедуре и далее о возможности сокращения [дерева] перебора вариантов, тем не менее трижды по ходу статьи приводит огромные цифры полуходов (те самые "квадриллионы операций"), которые необходимо рассмотреть, имеется ввиду программе, чтобы найти соответствующие варианты решения. Но эти-то цифры относятся к ПОЛНЫМ деревьям перебора!

Конечно, В.Городецкому трудно было и представить столь разительный прогресс как компьютерной техники, так и шашечных программ за последние три года. Однако, очень похоже на то, что он, как "чистый теоретик", просто не знает, на сколько реально может быть сокращено дерево перебора простым альфа-бета отсечением, тем более в сочетании с подходящей оценкой позиции (для "модельного терминального узла").

И, вообще, надо ли считать эти деревья до конца?

Для "экспериментов" мы использовали известную программу "Plus600", а также еще одну программу (назовем ее "DMaster"), подходящую для тестирования. Правильнее назвать ее альфа-версией, но вполне рабочей, с простой позиционной оценкой, альфа-бета отсечением, и задаваемой фиксированной глубиной перебора (число неударных полуходов) при расчете. И, естественно, без всяких библиотек.

Итак, проверяем позицию на диаграмме 1. Дерево перебора относительно неглубокое, и должно быть "по зубам" даже программе "DMaster". И действительно, правильный, хотя и казалось бы парадоксальный путь решения программа уверенно выбирает, начиная с глубины перебора 10 полуходов (513671 "просмотренных" позиций и 3 сек. на Pentium-II/350). То есть, "видит" из начальной позиции и необходимость и единственность варианта 3.hg3! f:h4 4.ba5. (В игре же достаточно было бы и глубины в 8 полуходов и долей секунды на ход, только программа "увидела бы" финальную жертву ходом позже...).

Следовательно, рассмотрение первой позиции позволяет сделать два вывода:

- для того, чтобы "отвергнуть" все варианты, кроме варианта-решения, вовсе не требуется осуществлять расчет на 22 полухода. Кстати, этот (самый длинный) в анализе вариант, после 2.fe3 ba5 однозначно должен отбрасываться при переборе с отсечением, раз есть вариант с тем же исходом, но короче (2... hg3).

- решить эту позицию должна ЛЮБАЯ компьютерная программа и, таким образом, ее можно рекомендовать в качестве тест-позиции для программы начального уровня.

Перейдем к более сложному примеру - позиции на диаграмме 2. "DMaster" смог найти только план 1... hd2!! за черных, позволяющий им сопротивляться. Дальше пришлось подключать программу "Plus600". Скажу сразу, что ей в итоге удалось найти выигрыш, но не так просто. Ход 5.fh6!! был найден достоточно быстро, а вот план с 6.ed8! и 8.d8-c7!! - только в режиме ретроанализа позиции, после нескольких часов (а не минут) "раздумий"...

Мы не будем описывать здесь подробно весьма интересный и поучительный процесс нахождения компьютерной программой истины, по одно простой причине - после хода 1... hd2 на доске остается только 6 фигур (на момент подготовки этого комментария мы располагали программой "Plus600" с 5-ти фигурной базой эндшпиля). А значит, большинству серьезных программ дальнейший поиск решения не требуется - готовое решение есть в 6-ти фигурной базе.

Не прошло и четырех месяцев со дня завершения III чемпионата России среди компьютерных программ, а уже, вслед за "Магистром", такой 6-ти фигурной базой эндшпиля обзавелись по крайней мере три программы - "Торнадо", "Тундра" и, совсем недавно, "Plus600". Так что и в эншпиле, подобном тому, который возник во второй позиции Городецкого, для компьютерных программ просто нет загадок!

Таким образом, современным компьютерным программам для игры в русские шашки вполне по силам обе позиции из данной статьи Городецкого. Но верен ли при этом вывод гроссмейстера о том, что расчет "убивает" эстетическую красоту шашек? Во-первых, можно привести и массу противоположных примеров. А во-вторых, отсечение вариантов, остающихся "за кадром", совсем не означает, что они отсутствуют в расчете! Это уже другой вопрос, который, кстати, поднимался на нашем Форуме, - вопрос того, зачем мы используем компьютерные программы, стоит ли им слепо доверять, и как правильно ставить им задачи...

Большей проблемой компьютерных программ мне представляется возможное "выхолащивание" игры вследствие использования только объективных или "абсолютных" оценок позиции (об оценке позиции см. статью рядом в этом разделе), отсутствие учета программами "человеческого фактора" и т.д. Но у меня почему-то есть уверенность том, что и эти проблемы преодолимы.

Вебмастер